Gomory's Cut Is Used as Which Method

By Ra_Ally543 12 May, 2022 Post a Comment

Cutting-plane methods were first developed by Ralph Gomory in the 1950s and Gomory Cuts remain among the basis of cutting-plane methods. Gomorys Cutting Plane Method Page 2 of 3 Daniel Guetta 2010 Inserting this inequality into our tableau we obtain x1 x2 x3 z1 z2 z3 z4 z5 x1 1 10 0 5 0 3 0 0 7 z2 0 5 0 2 1 1 0 0 5 x3 0 2 1 1 0 ½ 0 0 ½ z4 0 11 0 5 0 3 1 0 5 z5 0 2 1 1 0 1 0 1 0 0 31 0 8 0 3 0 0 23 The matrix in the body of the tableau is 1 B AA-.

How To Solve An Integer Programming Problem Using Cutting Plane Method Youtube

Any or all of the cuts can be added to the LP relaxation and the problem reoptimized.

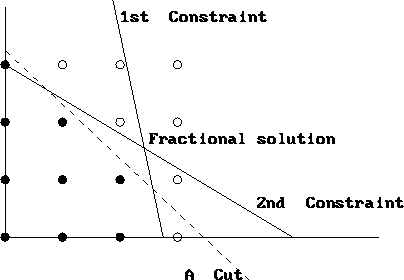
. Gomory Cutting Plane Algorithm. It is used in conjunction with the Simplex Method to generate optimal solutions to linear integer programming problems LIP. Used with permission Tutorial 11.

Gomorys Cut or Cutting Plane Method. Maximize Subject to Solving this with the simplex method gives the solution x 1 x 2 x 3 12 and the equations. 4 21 369.

Subject to 2x 1 4x 2 7 5x 1 3x 2 15. Given the system the Gomory Cut is defined as. Gomorys Cutting Plane method for AILP DERIVATION OF THE GOMORYS CUT CONSTRAINT 𝑀𝑎𝑥 𝑧 𝑐 𝑇 𝑥 subject to 𝐴𝑥 𝑏 𝑥 0 Eq.

The updated tableau is. All of the Gomory cuts are violated by the current basic feasible solution which has x3 x4 0. 1 𝑨 𝑩.

Maximize z x 1 4x 2. 𝑅 𝑥 𝐵 𝑥 𝑅 𝑏 𝐵𝑥 𝐵. However most experts including Gomory himself considered them to be impractical due to numerical instability as well as ineffective because many rounds of cuts were needed to make progress towards the solution.

Gomory cutting planes have been studied in depth and utilized in various commercial codes. Begin with LP in standard form for application of simplex method. Cutting planes were proposed by Ralph Gomory in the 1950s as a method for solving integer programming and mixed-integer programming problems.

One type of cutting plane is known as Gomory cutting planes. All of the Gomory cuts are violated by the current basic feasible solution which has x 3 x 4 0. X j a ij x j b i 3.

We choose to add with slack variable x 5. First solve the above problem by applying the simplex method try it yourselfThe final simplex table is presented below. The updated tableau is.

Gomory Algorithm Details. Gomory Cutting Plane Method. However most experts including Gomory himself considered them to be impractical due to numerical instability as well as ineffective because many rounds of cuts were needed to make progress towards the solution.

X2 51 11 1 11 s2 3 11 s3. The procedure is first ignore the integer stipulations and solve the problem as an ordinary LPP. Example Applying a Gomory Cut to the Simplex Method.

Let a be greatest integer a rounding down and de ne the fractional part of a to be a a. However most experts including Gomory himself considered them to be impractical due to numerical instability as well as ineffective because many rounds of cuts. We will show that by using exact arithmetic rather than floating point arithmetic we can produce better cuts.

Generate a Gomory cut and add it to the LP formulation With careful choice of LP solvers and cut generation the algorithm can be shown to terminate in nite time. Each of these equations produces the same cutting plane and with the introduction of a new slack variable x 7 it can be. X 1 x 2 are integers 0.

If the solution satisfies the integer restrictions then an optimal solution for the original problem is found. Cutting planes were proposed by Ralph Gomory in the 1950s as a method for solving integer programming and mixed-integer programming problems. Maximize Subject to Introduce slack variables x i i4 5 6 to produce the standard form.

For the next Gomory cut we use the third row. GOMORYS CUTTING PLANE ALGORITHM CONT. X1 x2 x3 x4 x5 71 14 0 0 1 14 3 14 0 23 7 0 1 2 7 1 7 0 25 14 1 0 3 14 5 14 0 11 14 0 0 11 14 5 14 1.

Cutting-plane Method - Gomorys Cut. We introduce a new slackness variable s4 and a new constraint 1 11 s2 8 11 s3 s4 7 11. Note that x 5 must also be integral.

For optimization the most important add-in is Excel Solver which can be used to solve a wide range of optimization problems. So the cut is 7 11 1 11 s2 8 11 s3 0. Historically the first method for solving IPP.

Things turned around when in the mid-1990s Gérard Cornuéjolsand co-workers showed them to. Any or all of the cuts can be added to the LP relaxation and the problem reoptimized. Gomorys Cut Cutting planes were proposed by Ralph Gomory in the 1950s as a method for solving integer programming and mixed-integer programming problems.

Optimization Methods in Management Science. Gomory cuts and a little more PDF. Suppose Gomorys algorithm is implemented by 1using the lexicographic simplex algorithm for LP solving and 2deriving Gomory cut from the fractional variable.

Was the cutting plane method. Apply simplex method until convergence and select any noninteger b i constraint. AN EXAMPLE OF THE GOMORY CUTTING PLANE ALGORITHM 5 11 11 11 This is optimal and LP-feasible but not integral.

Note that x5 must also be integral. 𝑹 𝒙 𝒄𝒐𝒍 𝒙 𝑩 𝒙 𝑹 𝒄 𝒄𝒐𝒍 𝒄 𝑩 𝒄 𝑹 𝐴𝑥 𝑏 𝐵. 2 The basic definition of a Gomory Cut is as follows.

Gomorys Cut or Cutting Plane Method. We choose to add 2 with slack variable x5. Consider the integer optimization problem.

A extendA110. This method is for the pure integer programming model. The expressiveness of Excel comes at the cost of having a long learning curve.

A Gomorys Cut is a linear constraint with the property that it is strictly stronger than its Parent but it does not exclude any feasible integer solution of the LP problem under consideration. The main reason for this is the addition of slack variables to the Gomory inequalities.

Cutting Plane Method Wikiwand